Задача. На некотором интервале заданы экспериментальные точки. Предполагается, что из каких-то сторонних исследований известна форма функции y(t), которая примерно описывает исследуемый процесс. Необходимо подобрать численные параметры этой функции, что бы ее значения были близки к заданным экспериментальным точкам.
Так же предполагается, что известные экспериментальные точки это не точные значения функции y(t), а значения с добавлением некоторого шума z(t)=y(t)+noise(t).
На рисунке ниже пример экспериментальных точек, для которых нужно подобрать аналитическое выражение.
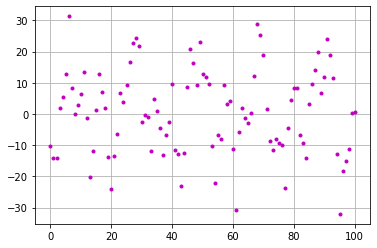
Предположим, что из предварительного анализа процесса известно, что процесс гармонический и предположительно описывается тремя гармониками, амплитуда, частота и фаза которых не известны.
О том, что процесс носит гармонический характер можно сделать интуитивный вывод по виду картины распределения экспериментальных точек.
Таким образом, требуется найти три амплитуды, три частоты и три фазы, которые не известны. Для этого могут быть использованы функции библиотеки scipy.optimize. За критерий близости получаемой аналитической зависимости к экспериментальным точкам принимаем коэффициент детерминации (R squared). Требуется обеспечить такие цифровые параметры функции, при которых разница между коэффициентом детерминации и единицей будет минимальной.
Функция basinhopping.
Функция предназначена для поиска глобального минимума. Работает относительно медленно.
Функция реализует двух-этапный метод, который сочетает в себе глобальный алгоритм с локальной минимизацией на каждом шаге. Разработанный для имитации естественного процесса минимизации энергии кластеров атомов, он хорошо работает для аналогичных задач с “воронкообразными, но изрезанными” энергетическими ландшафтами.
На рисунке ниже аппроксимация заданных экспериментальных точек суммой трех гармонических функций с параметрами оптимизированными функцией minimize..
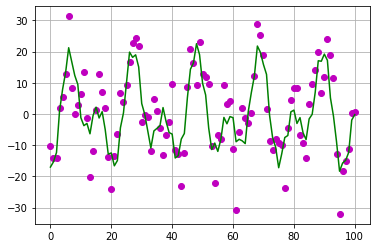
Полученный коэффициент детерминации примерно 0.64.
Функция minimize.
Функция предназначена для поиска локального минимума. Работает существенно быстрее функции basinhopping. Но приближение к экспериментальным точкам может быть существенно хуже из-за провала в локальный минимум. При удачном выборе начальной точки результаты обоих функций будут близки.
На рисунке ниже аппроксимация заданных экспериментальных точек суммой трех гармонических функций с параметрами оптимизированными функцией minimize.
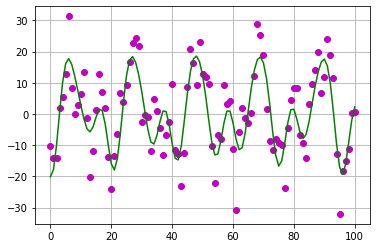
Источники
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.basinhopping.htm