Модель простого маятника реального практического интереса не представляет. Однако, на этой простой модели удобно отрабатывать различные идеи моделирования и фильтрации данных.
Модель простого маятнике может описывать реальные простые физические объекты, например:
- Механический маятник имеющий относительно длинный подвес;
- Груз на пружине;
- Электрический LCR контур.
Дифференциальное уравнение, описывающее затухающий осциллятор:
D2x + 2*Gamma*Dx + Omega0^2*x = 0
Где
2*Gamma = Alpha / m, Gamma – постоянная затухания, размерность частоты
Omega0 = sqrt(k / m) — собственная частота системы
OmegaF = sqrt(Omega0^2 – Gamma^2) — частота свободных колебаний
Добротность (безразмерный параметр)
Q= Omega0 / 2*Gamma
Добротность, меньшая или равная 0,5, соответствует неколебательному движению осциллятора; в свободном движении он пересечёт положение равновесия не более одного раза.
Время затухания (время релаксации) — время, за которое амплитуда колебаний уменьшится в e раз
Tau = 1 / Gamma
На рисунке ниже показано отклонение от равновесия простого осциллятора (маятника) от точки равновесия после его смещения от точки равновесия.
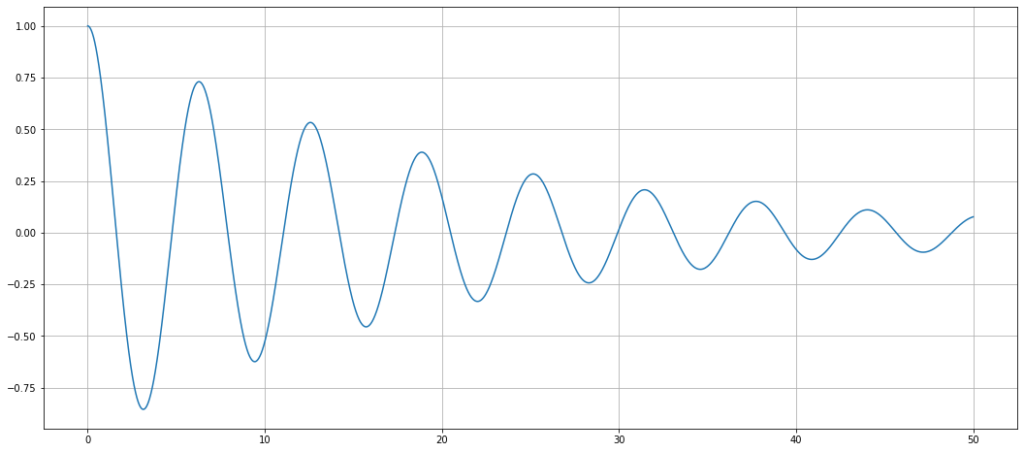
На следующем рисунке тот же осциллятор (маятник), который находился в состоянии равновесия и периодически подвергается случайным толчкам.
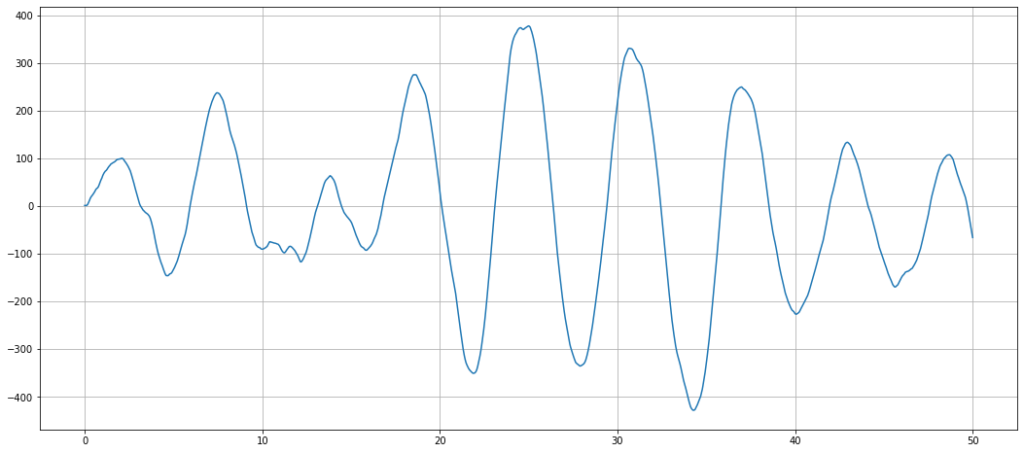
Для работы с системы, возбуждаемой случайными воздействиями, может быть применен фильтр Калмана.
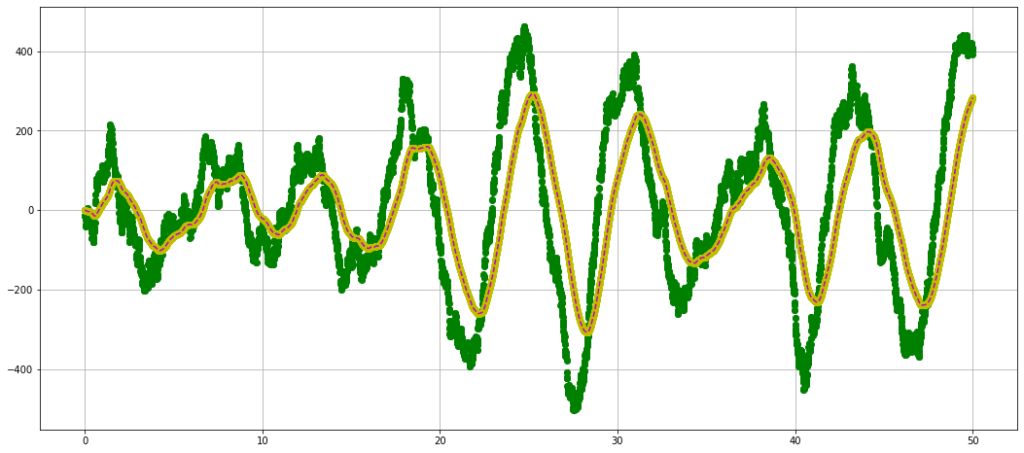
На графике ниже показана зависимость реального отклонения осциллятора — зеленые кружки, которые слились в полосу.
Отклонение осциллятора, оцененное фильтром Калмана — желтая линия в середине зеленой полосы.
Отклонение осциллятора, оцененное фильтром Калмана на этапе экстраполяции — малиновый пунктир, расположенный практически на желтой линии.
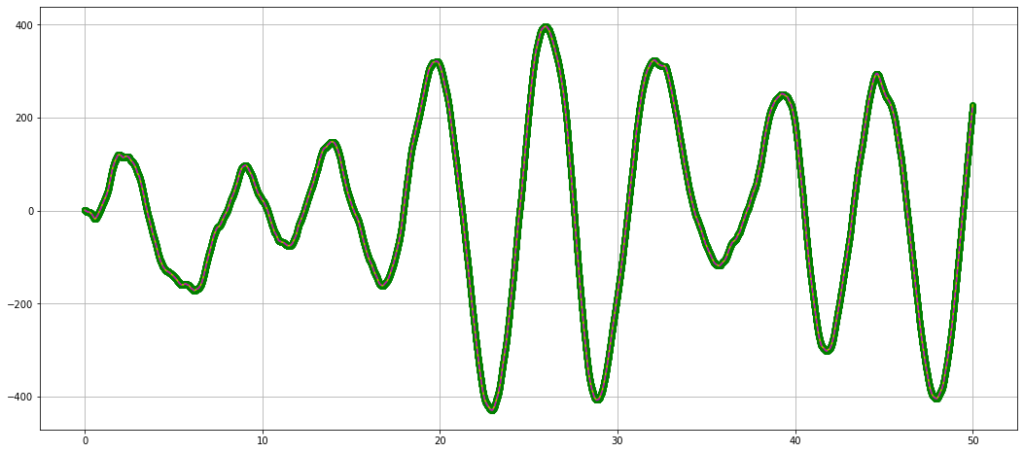
На графике ниже показана разность между реальным отклонением осциллятора и оценкой фильтром Калмана — зеленый пунктир.
Красные точки — разность между реальным отклонением осциллятора и оценкой фильтром Калмана на этапе экстраполяции
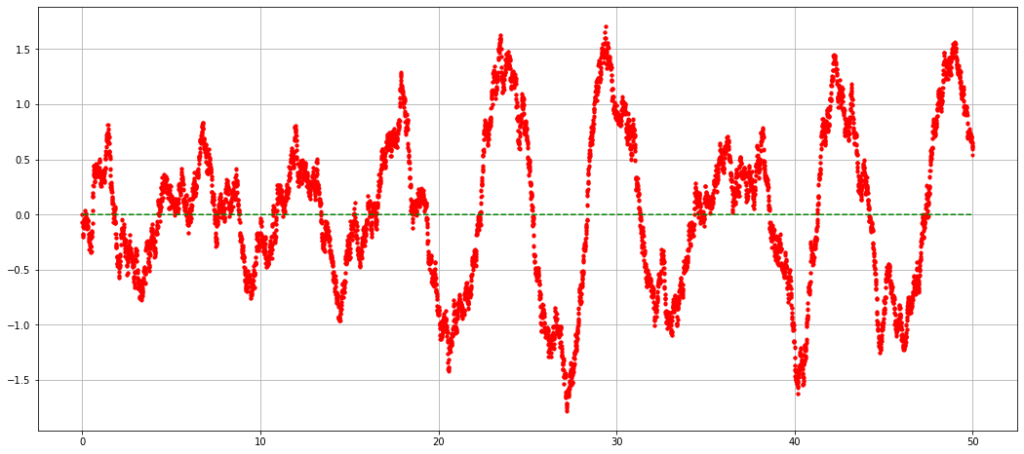
На графике ниже показана зависимость реальной скорости осциллятора — зеленые кружки, которые слились в полосу.
Скорость осциллятора, оцененное фильтром Калмана — желтые кружки, которые слились в полосу.
Скорость осциллятора, оцененное фильтром Калмана на этапе экстраполяции — малиновый пунктир, расположенный практически на желтой полосе.
NB Замер скорости осциллятора не подавался в фильтр Калмана
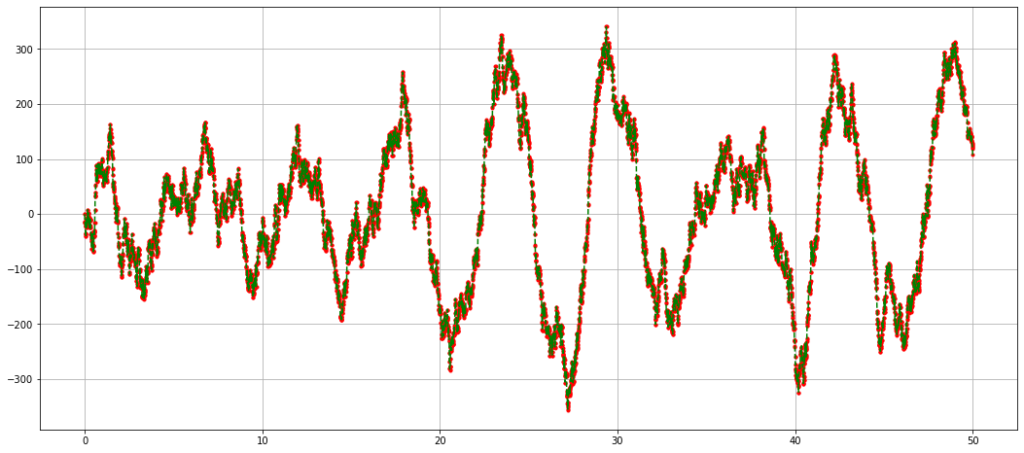
На графике ниже показана разность между реальной скоростью осциллятора и оценкой фильтром Калмана — зеленый пунктир.
Красные точки — разность между реальной скоростью осциллятора и оценкой фильтром Калмана на этапе экстраполяции.
Пример решения уравнения осциллятора с затуханием методом Эйлера и его поведение при воздействии случайного возмущения (на языке Python) приведен в файле:
В том же примере показана возможность использования фильтра Калмана для наблюдения да функционированием осциллятора.